极坐标计算器

极坐标系统

极坐标系是一种二维坐标系，其中平面上的每个点由与参考点的距离和与参考方向的角度确定

参考点称为极点，来自极点在参考方向上的光线是极轴。与极点的距离称为径向坐标、径向距离或简称半径，角度称为角坐标、极角或方位角。极坐标符号中的角度通常以度或弧度表示。

在数学中，参考方向通常绘制为从极点水平向右（沿x轴）的射线，并且逆时针旋转的极角增加。对于相反方向的旋转，极角向负值减小。 θ

另一方面，正如我们所知，平面上的矩形或笛卡尔坐标是一对数字，分别沿 x 轴和 y 轴测量。这两个轴彼此垂直。平面上的每个点都可以由这对坐标确定。 x  y  P

极坐标可以通过三角函数正弦和余弦转换为笛卡尔坐标和：

x=r⋅cosθ， y=r⋅sin θ.

笛卡尔坐标可以转换为极坐标，并且使用以下公式在区间 （−，] 中≥ 0 和 （−，] 中：

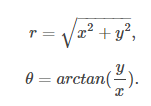
首先按上述方式计算 ifis，然后公式 for可以使用反余弦函数更简单地表示： r  θ

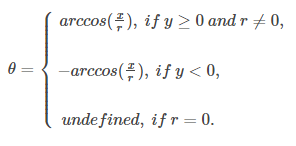
这些公式用于我们的极坐标计算器，这使得坐标变换只需几分之一秒。